Matrix gradient

chain rule 이란, 함수의 연쇄법칙으로

합성함수 F = f(g(x)) 의 미분 F’=f’(g(x))g’(x)등을 의미한다.

NER에서, 두번의 hidden layer를 거쳐 하나의 scalar 값(s)을 내보내게 되는데,

이때 weight matrix인 W에서의 미분을 보게 되면

∂s/∂W = ∂s/∂h * ∂h/∂z * ∂z/∂W
이때 s = u^T h, h=f(z), z=Wx+b

와 같이 계산할 수 있다.

이후 계산은 아래 슬라이드 캡쳐와 같다.

fig

word vector에서는 아래와 같다.

fig

Backpropagation

fig

위와 같이 앞으로 넘어오는 에러를 어떻게 찾아낼 수 있을까 ?

(이미지)

output을 input에 대해 미분한 ‘local gradient’를 통해 에러를 찾을 수 있다!

위에서 upstream에 local gradient를 곱해 downstream을 도출한다 (chain rule)

multiple input에서는, input의 개수만큼 local gradient를 계산해준다.

fig

또한 일반적으로 사용되는 numerical gradient는 매번 f를 새로 계산해야하므로

computation graph보다 매우 느려서, 일부에 대해서 계산이 올바른지 확인하는 용도로 쓰인다.

loss function을 그냥 쓰면 overfitting의 위험이 있지만, regularization을 더해주면 이를 막을 수있다.

fig

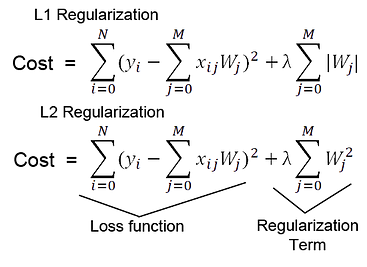
특히 feature가 많은 깊은 모델일수록 효과가 좋다

fig

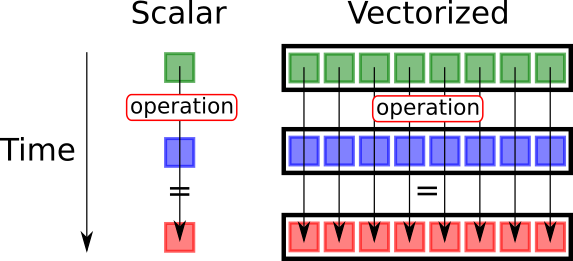
이렇게 vectorize (matrix화)하여 계산하면 훨씬 efficiency하게 계산할 수 있다

fig