Regression

여러개의 feature(predictor variable)를 사용해 target을 예측하기

Linear Regression, Desicion Tree, Random Forest …

- e.g. spam filter

일부 regression은 classification에 이용 가능 (e.g. Logistic Regression)

Classification

classifier를 이용하여 binary 또는 multi-class, multi-label 분류 실행하기

코드 reuse하여 새로운 dataset에 적용 ⭕️ here

Model traning (Chap 4)

Linear regression

training set에 가장 잘 맞는 선형 모델

즉, y = B0 + B1*x 에 적당한 parameter(B0, B1) 를 찾는 과정을 모델 학습 과정이라고 함

(이때, 식을 벡터 형태로 나타내기도 함 )

이때, 성능 측정을 위해 RMSE을 이용한다 ( RMSE를 최소화하는 parameter를 찾아야 한다 )

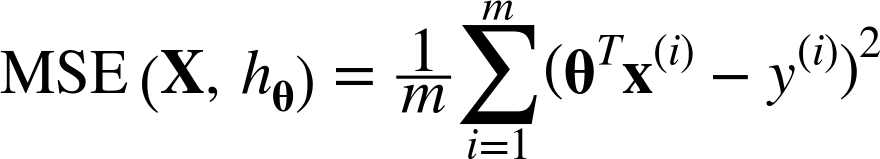
- 훈련 시키는 방법

1. 직접 계산

• normal equation을 이용하기

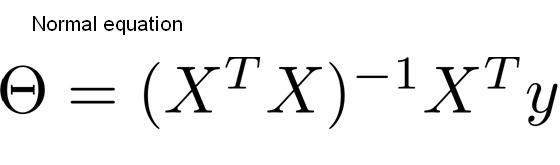
- 이 경우, training set의 noise 때문에 정확한 계산이 힘듦

• Least squares 를 이용하기 (오차의 제곱이 작아지도록)

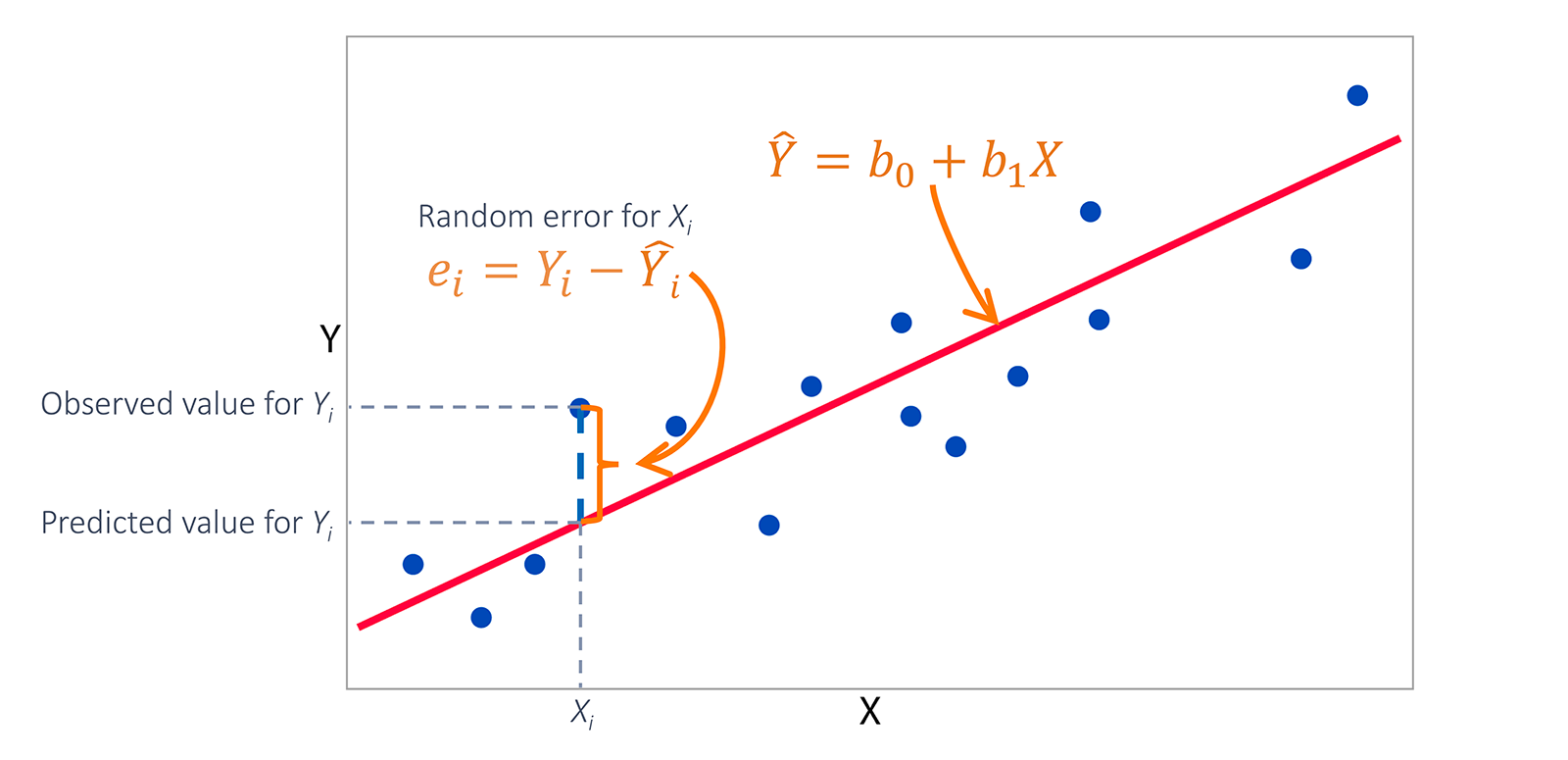
• sklearn.linear_model.LinearRegression() 이용하기

  • 이때, Singular Value Decomposition 을 이용하여 pseudo-inverse 구하기

2. Gradient Descent 이용하기 (GD, batch GD, mini-batch GD, SGD)

cost funtion(loss function)을 최소화하기 위해 반복적으로 parameter를 조정

이 때, cost function의 현재 gradient를 계산하여, gradient가 감소하는 방향으로 진행

-> 만약 gradient == 0이면, 최소값에 도달할 수 있음

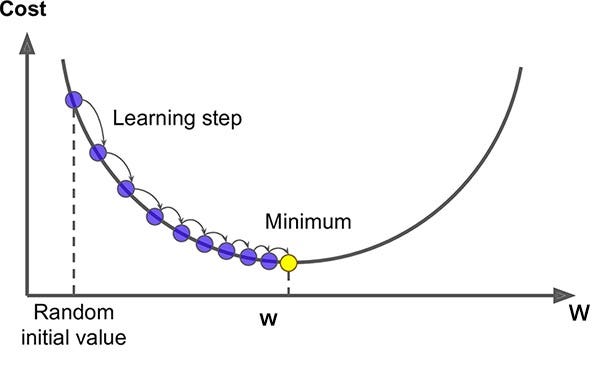
 1. random하게 parameter 초기화

 2. step 크기(learning rate)만큼 이동 - step 크기는 cost function의 기울기에 비례

 3. 최소값 찾기

• 이때 local minimum에 빠질 수 있지만, linear regression에서의 MSE cost funtion은 convex해서 문제 x

• feature의 scale이 지정되지 않으면, cost funcion의 모양이 길쭉해져 minimum 찾기 힘듦

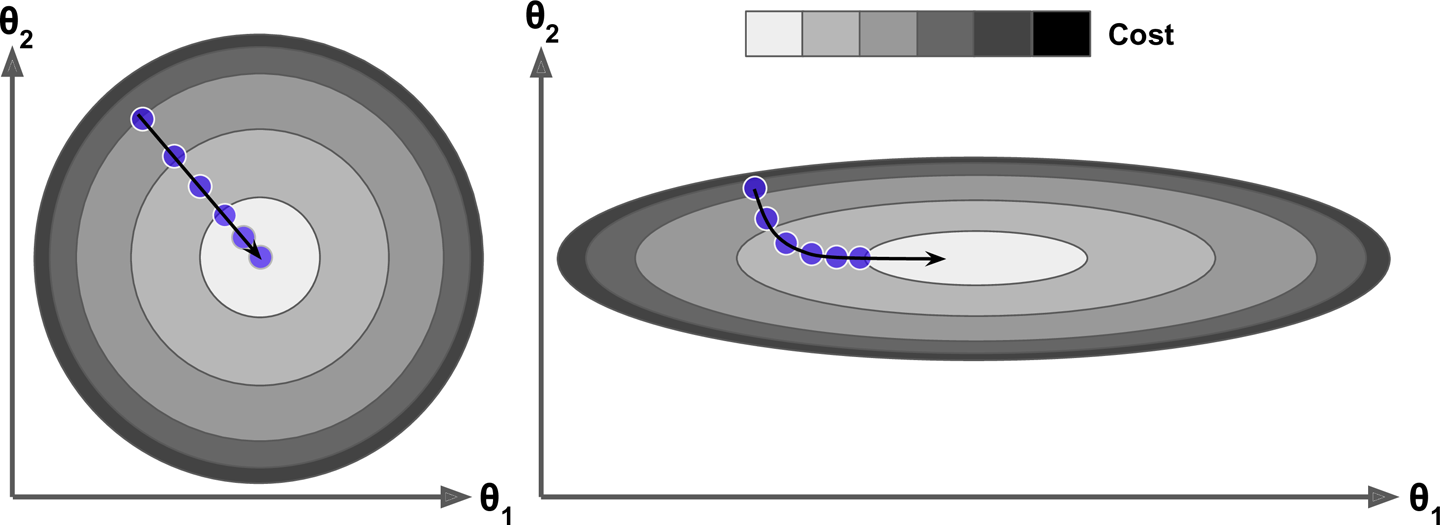
• model의 parameter가 많을수록 최적의 parameter를 찾을 수 있는 parameter space의 차원이 커지고 검색이 힘듦

• 편도함수(partial derivative)

parameter가 편할때마다 cost funtion이 변하는 정도

아래와 같이 cost function을 미분해서 기울기의 편화를 관찰한다. parameter가 많으면 벡터로 연산이 가능하다

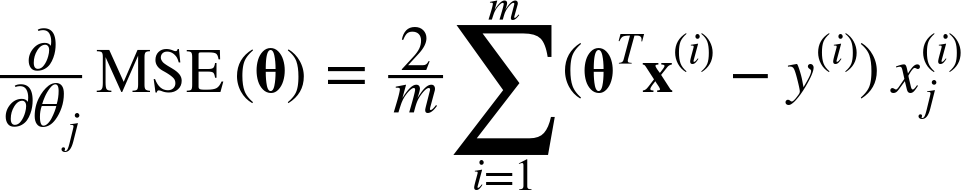
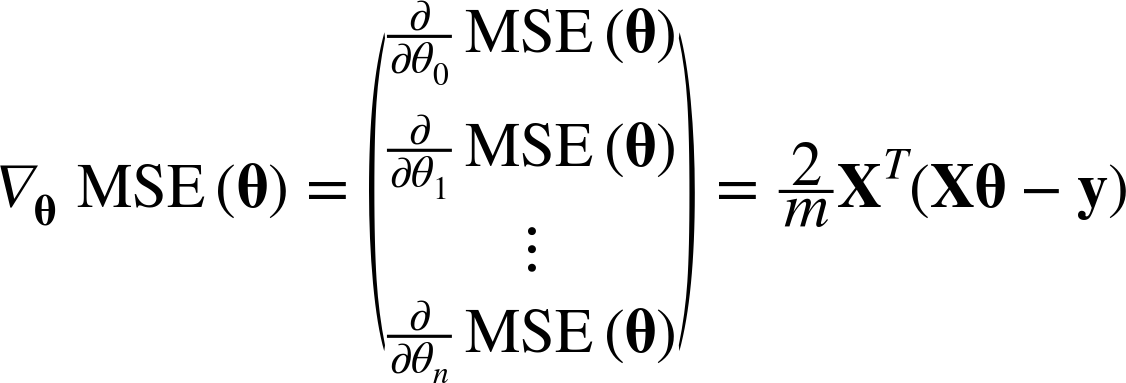
-> 이렇게 gradient가 구해지면, 반대방향으로 가야(벡터에 음수를 더해야) 하는데,

이때 얼마나 가야 할지를 정하기 위해 learning rate를 계산한다.

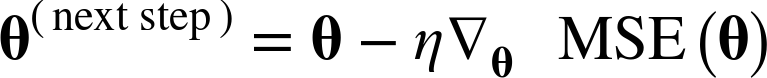
반복횟수를 크게 지정하고, gradient 벡터가 작아지면 (벡터의 norm이 허용 오차 tolerance보다 작아지면) GD가 최소값에 도달 -> 알고리즘 중단

1) Batch Gradient Descent

모든 step에서 전체 training data를 사용함

• feature 개수에 민감하지 않음

• data 수가 크면 매우 느림

2) Stochastic Gradient Descent)

매 step에서 한개의 sample을 무작위로 선택하고, 그 하나의 sample에 대한 gradient 계산

• 속도 빠름

• 무작위(확률적)이기 때문에 불안정함 - global minimum을 못찾거나 건너뛸수도 있음

이를 해결하기 위해 learning rate를 점진적으로 감소시키기 # learning schedule 조절

from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())

3) Mini-batch Gradient Descent

mini-batch라 부르는 임의의 작은 sample set에 대해 gradient를 계산

• mini-batch를 어느정도 크게 하면 parameter space에서 SGD보다 덜 불규칙하게 움직임

• local minimum에서 빠져나오기 힘들수도 있음

*Linear regression with Regulation

overfitting을 줄이기 위한 regulation 추가

linear regression의 경우 주로 model의 weight를 제한

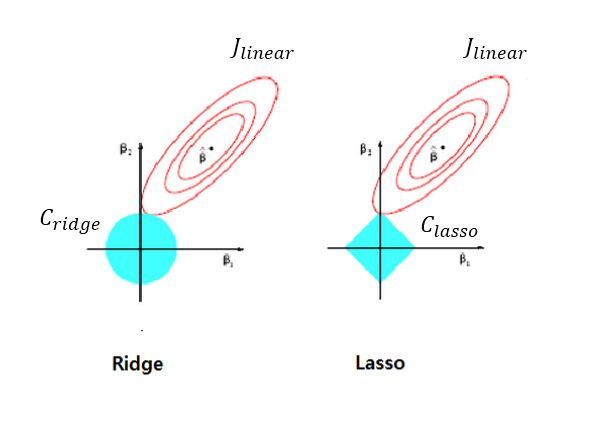
1. Ridge regression

squared sum of weights)을 최소화하는 것을 추가적인 제약 조건으로 한다

𝜆 는 기존의 잔차 제곱합과 추가적 제약 조건의 비중을 조절하기 위한 hyper parameter이다.

𝜆가 크면 정규화 정도가 커지고 가중치의 값들이 작아진다. 𝜆가 작아지면 정규화 정도가 작아지며 𝜆 가 0이 되면 일반적인 선형 회귀모형이 된다.

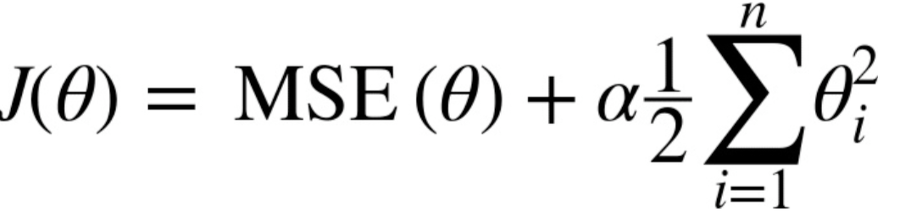
2. Lasso regression

가중치의 절대값의 합을 최소화하는 것을 추가적인 제약 조건으로 한다.

이때, 상대적으로 덜 중요한 feature의 가중치를 제거하려고 한다

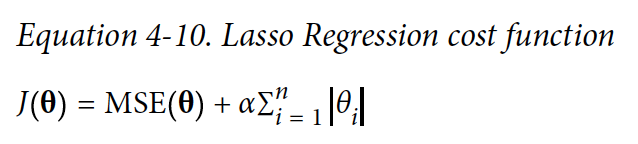
이렇게 parameter = 0일때 원래는 미분 가능하지 않지만, subgradient vector를 이용하면 GD 적용 가능

3. Elastic net regression

ridge와 lasso를 절충한 model

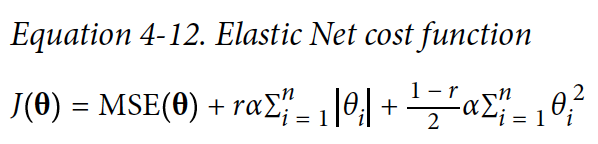
또는 에러가 최소값에 도달하면 earling stopping

Polynomial regression

linear 하지 않고 복잡한 형태의 dataset 일때,

각 feature의 거듭제곱을 새로운 feature로 추가하고, 이를 포함한 dataset에 linear model을 훈련시키는 것

이때 sklearn.preprocessing.PolynomialFeatures()의 degree를 조절함으로서 a^2b, a^2b^4 등등 다양한 feature를 추가할 수 있음

* 학습 곡선

model의 성능 확인을 위한 방법 중 하나

training set와 validation set의 모델 성능을 training set 크기의 함수로 나타냄

-> training set에서, 크기가 다른 subset를 만들어 모델을 여러번 훈련시키기

-> x축은 training set 크기, y축은 RMSE 인 그래프 생성

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
    X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
    train_errors, val_errors = [], []
    for m in range(1, len(X_train)):
        model.fit(X_train[:m], y_train[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_val)
        train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
        val_errors.append(mean_squared_error(y_val, y_val_predict))
    plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="훈련 세트")
    plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="검증 세트")

* vias variance trade-off

일반적으로 모델의 복잡도가 커지면 variance가 늘어나고 bias가 줄어듦

모델의 복잡도가 작아지면 variance가 작아지고 bias가 커짐

Logistic Regression

classification도 가능한 regression model algorithm

즉, sample이 특정 class에 속할 확률을 추정하는데 사용 -> 확률이 50%가 넘으면 해당 class에 속한다고 예측

• 이때 sigmoid function을 이용

- 즉 z의 값에 따라 양수이면 확률(y)이 0.5이상, 음수이면 확률(y)이 0.5 이하 `# binary classification `

따라서, model을 훈련시키기 위해서는 해당 class에 속할 확률을 높게 추정하게끔 해야함

-> log loss를 cost funtion으로 이용함

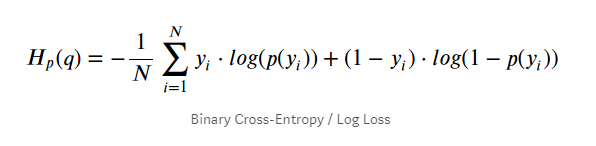
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)

* Softmax Regression (Multinomial Logistic Regression)

2개 이상의 다중 class를 분류할 수 있는 모델

1. softmax regression model이 먼저 각 class에 대한 점수 계산
2. 계산한 점수에 sormax funtion을 적용하여 각 class의 확률 추정

• softmax regression classifier의 예측

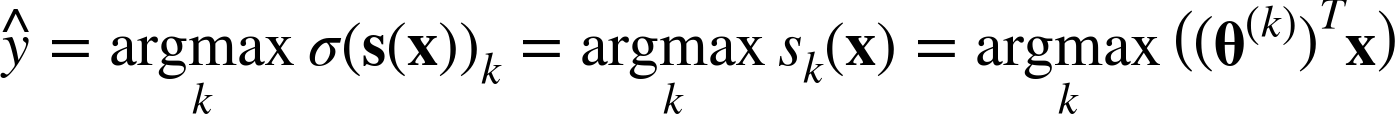
- `argmax` 연산은 함수를 최대화하는 변수의 값을 return

이때, cost function으로 cross entropy를 이용함

(추정된 class의 확률이 target class에 얼마나 잘 맞는지 측정하는 용도)

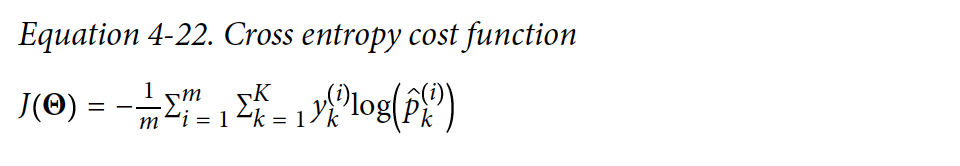
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)
softmax_reg.fit(X, y)

Reference

• <Hands-On Machine Learning 2> Chap 3,4