Midannii's

🍳 reference: <모두를 위한 딥러닝 2: pytorch> Lab6

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

Softmax

soft하게 max값을 뽑아주는 함수

$fig$

z = torch.FloatTensor([1, 2, 3])
hypothesis = F.softmax(z, dim=0)
print(hypothesis)
# tensor([0.0900, 0.2447, 0.6652])

원래 max는 0,0,1을 출력하지만 softmax는 합쳐서 1이 되도록 출력함

Cross Entropy

두 확률 분포가 얼마나 비슷한지를 나타내는 함수

fig

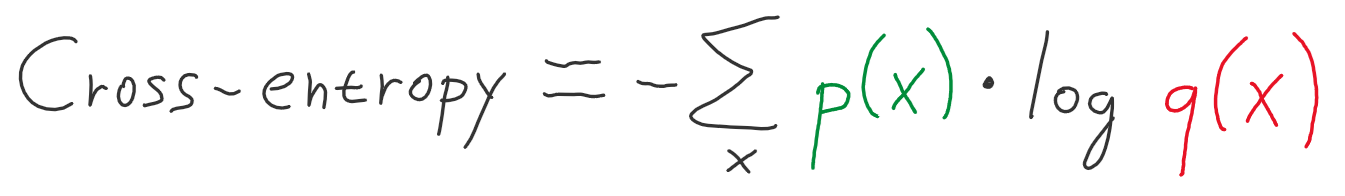
cross entropy loss

$fig$

z = torch.rand(3, 5, requires_grad=True) # 3개의 sample, 5개의 class
hypothesis = F.softmax(z, dim=1)
print(hypothesis)
#tensor([[0.2645, 0.1639, 0.1855, 0.2585, 0.1277],
#        [0.2430, 0.1624, 0.2322, 0.1930, 0.1694],
#        [0.2226, 0.1986, 0.2326, 0.1594, 0.1868]], grad_fn=<SoftmaxBackward>)

discret 하므로, 이를 one-hot vector로 표현해주자

y_one_hot = torch.zeros_like(hypothesis)
y_one_hot.scatter_(1, y.unsqueeze(1), 1) #  각각 dim = 1에 대해, y.unsqueeze(1)에 1을 뿌리기
                                      ### 즉, [0,2,1]이 아래와 같이 변함

#tensor([[1., 0., 0., 0., 0.],
#        [0., 0., 1., 0., 0.],
#        [0., 1., 0., 0., 0.]])

cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
print(cost)
# tensor(1.4689, grad_fn=<MeanBackward1>)

위에서, -torch.log(hypothesis))는 (3,5)이지만, sum(dim=1)을 적용함으로서 (3,)이 됨

이후 mean()의 결과 하나의 숫자로 결과를 반환

model.nn 을 이용하면 아래와 같다

# Low level
torch.log(F.softmax(z, dim=1))

# High level
F.log_softmax(z, dim=1)

또한 log Likelyhood는

# Low level
(y_one_hot * -torch.log(F.softmax(z, dim=1))).sum(dim=1).mean()
# tensor(1.4689, grad_fn=<MeanBackward1>)

# High level
F.nll_loss(F.log_softmax(z, dim=1), y)
#tensor(1.4689, grad_fn=<NllLossBackward>)

이때 NLL은 Negative Log Likelyhood 이다.

그러나 cross_entropy() 를 이용하면 softmax와 NLL을 모두 한번에 처리할 수 있다

F.cross_entropy(z, y)
#tensor(1.4689, grad_fn=<NllLossBackward>)

Implementation

전체 학습 코드는 아래와 같다.

아래의 경우는 m개의 sample, 3개의 class, 4-dimension 이다.

x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 2, 5, 6],
           [1, 6, 6, 6],
           [1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)

# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # Cost 계산 (1)
    hypothesis = F.softmax(x_train.matmul(W) + b, dim=1) # or .mm or @
    y_one_hot = torch.zeros_like(hypothesis)
    y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)
    cost = (y_one_hot * -torch.log(F.softmax(hypothesis, dim=1))).sum(dim=1).mean()

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

위에서 Cost 계산 부분만 아래 코드로 대체 가능하다

# Cost 계산 (2)
z = x_train.matmul(W) + b # or .mm or @
cost = F.cross_entropy(z, y_train)

또는 SoftmaxClassifierModel()를 사용하면 아래와 같다

model = SoftmaxClassifierModel()

# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # H(x) 계산
    prediction = model(x_train)

    # cost 계산
    cost = F.cross_entropy(prediction, y_train)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 20번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))