SVM은 linear, nonlinear classification이나 regression, outlier detection 등등 다양한 용도로 쓸 수 있는 모델이다.
특히 복잡한 classification 문제에 잘 맞으며, 크지 않은 dataset에 적합하다.
SVM classification
SVM classifier는 class에 대한 확률을 제공하지 않는다.
linear SVM classification
쉽게 생각하면 class 사이에 가장 폭이 넓은 도로를 찾는 것이다. (large margin classification)
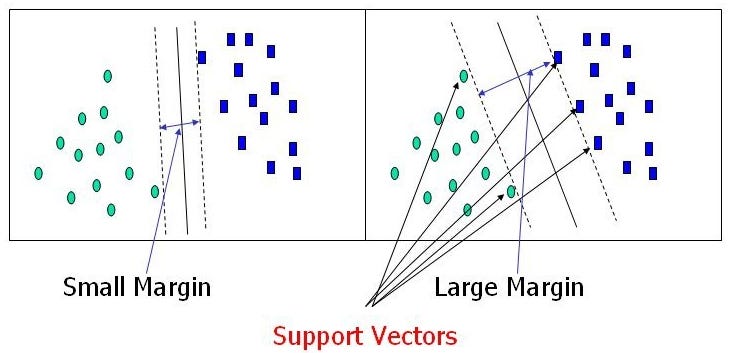
이때 도로 바깥에 샘플을 더 추가해도 결정 경계에는 영향을 미치지 않는데, 이를 suppor vector라고 한다.
이러한 SVM은 특성의 scale에 민감하므로, sklearn.StandardScaler를 사용하면 결정 경계가 확실히 좋아진다.
모든 sample이 도로 바깥쪽에 올바르게 분류되면 hard margin classification이라고 한다.
그러나 이 경우 linear한 데이터에만 작용하며, outlier에 민감하다는 단점이 있다.
이를 보완할 수 있는 것이, 도로의 폭을 넓게 유지하는 것과 margin violation(마진 오류)의 균형을 잡는 soft margin classification이라고 한다.
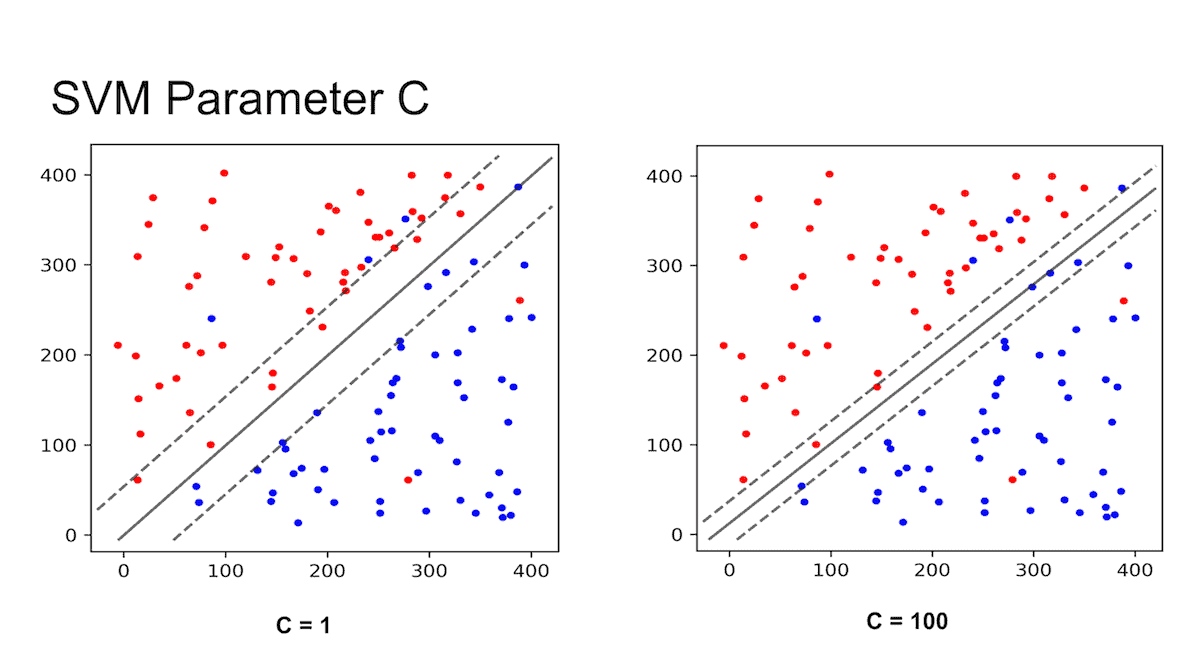
sklearn.svm에서, hyperparameter인 c를 작게 설정할수록 margin 경계가 커지고, 마진 오류가 많아진다.
그러나 일반화를 더 잘할 수 있어 overfitting을 규제할 수 있다.
아래는 svm classifier의 예제 코드이다.
from sklearn import datasets
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # 꽃잎 길이, 꽃잎 너비
y = iris["target"]
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
# SVM 분류 모델
svm_clf = SVC(kernel="linear", C=1) # 또는 LinearSVC(C=1, loss="hinge")
svm_clf.fit(X, y)
또는 SGDClassifier(loss='hinge', alpha = 1/(m*C)) 를 이용해도 된다.
Theory
결정 함수 wTx+b = w1x1+ … + wnxn + b를 를 계산해서 새로운 샘플 x의 클래스를 예측한다.
결괏값이 0보다 크면 예측된 클래스 yˆ은 양성 클래스, 그렇지 않으면 음성 클래스(0)가 된다.
예를들어 iris dataset의 경우, feature가 두 개(꽃잎의 너비와 길이)인 데이터셋이기 때문에 2차원 평면이다.
결정 경계는 결정 함수의 값이 0인 점들로 이루어져 있고, 두 평면의 교차점으로 직선이다(굵은 실선).
linear SVM classifier 를 훈련한다는 것은 마진 오류를 하나도 발생하지 않거나(hard margin)
제한적인 마진 오류를 가지면서(soft margin) 가능한 한 margin을 크게 하는 w와 b를 찾는 것.
nonlinear SVM classification
nonlinear dataset을 다루는 방법은 다항식 feature을 더 추가하는 것이다.
예를 들어, y = x^2이 있으면 t = x^2으로 두어 y = t를 만들 수 있다.
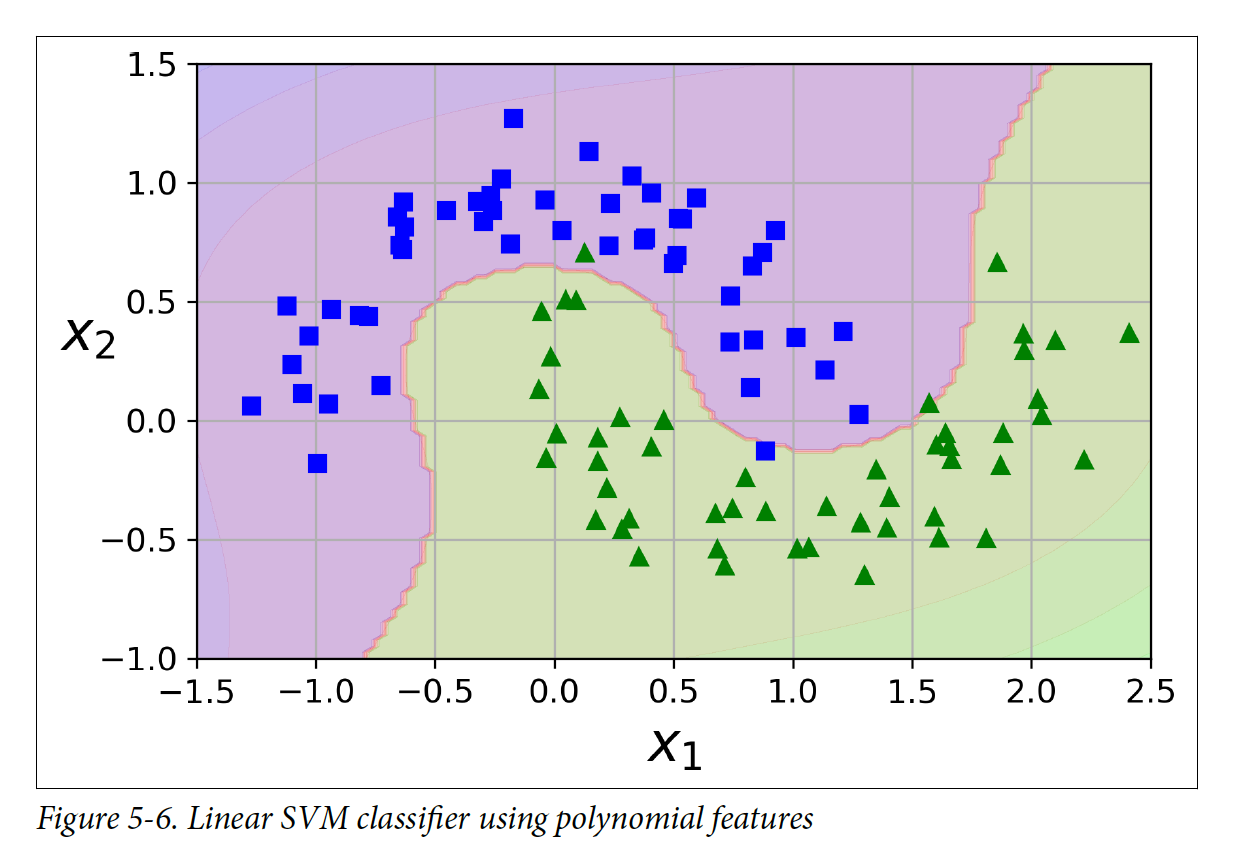
코드는 아래와 같다.
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
])
polynomial_svm_clf.fit(X, y)
Kernel trick
차수가 낮은 다향식 feature 를 추가하면 복잡한 dataset을 잘 설명하지 못하고, 모델을 느리게 만들 수 있다.
이를 해결하기 위한게 kernel trick 인데, 실제로는 feature을 추가하지 않으면서 다항식 feature을 많이 추가한 것과 같은 결과를 얻을 수 있다.
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5)) # 3차 다항식 kernal을 이용
])
poly_kernel_svm_clf.fit(X, y)
overfitting이면 차수를 줄이고, underfitting이면 차수를 높여야 한다.
사용 가능한 커널들은 위와 같다.
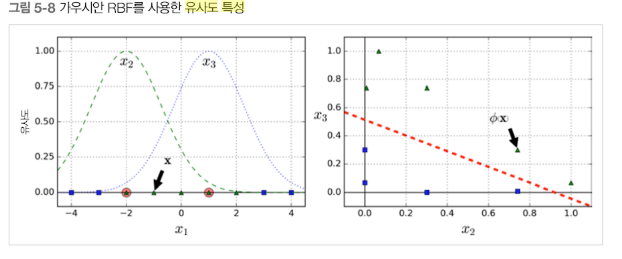
유사도 특성 (similarity feature)
각 샘플이 특정 landmark와 얼마나 닮았는지를 측정하는 similarity funtion으로 계산한 feature를 유사도 특성이라고 하고, 이를 추가하기도 한다.
이때 r = 0.3인 가우시안 방사 기저 함수 (RBF)를 similarity function으로 정의한다.
이를 이용한 코드는 아래와 같다.
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)
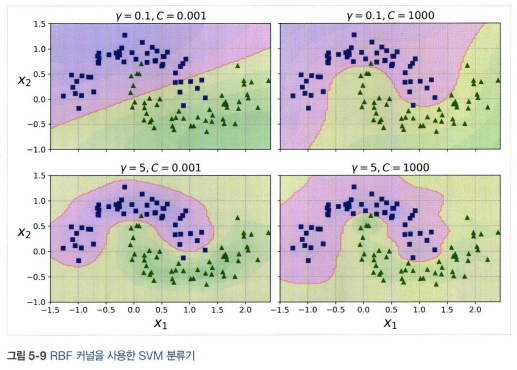
이처럼 gamma와 c를 바꿔가며 훈련시킨다.
SVM regression
linear/nonlinear regression을 수행할 수 있으며, 이 경우 classification의 목표와 반대로 작용한다.
제한된 마진 오류(즉, 도로 밖의 샘플) 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습하며, 도로의 폭은 hyperparameter ε으로 조정한다.
(이때 ε에 따라 모델의 예측에 상관없는 경우 ε-insensitive라고 한다.)
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)
c에 따라 규제를 설정할 수 있다.